Volumetric Path Tracing on CPU and GPU

CS184 Final Project by Yin Tang, Jimmy Xu, Yi Zong

Abstract

In this project, we utilized raymarching algorithm to implement a volumetric path tracer on CPU. We then used part of beam radiance estimate and Nvidia OptiX ray tracing engine to make the volumetric path tracer interactive.

Background

The vanilla path tracing algorithm assumes light only scatters when it hits a surface. However, it is not always the case in the real world as shown in the picture below. The cause of such effect is that a ray may get scattered before it hits any surface in volume. To model this effect, the path tracer needs to take participating media into account and then computes an integral over all volumes and all surfaces to calculate the final radiance.

Intuitively, this procedure is therefore even more computationally expensive than normal path tracing so it is worth utilizing GPU to shorten the rendering time.

Raymarching Volumetric Path Tracer on CPU

Raymarching Algorithm

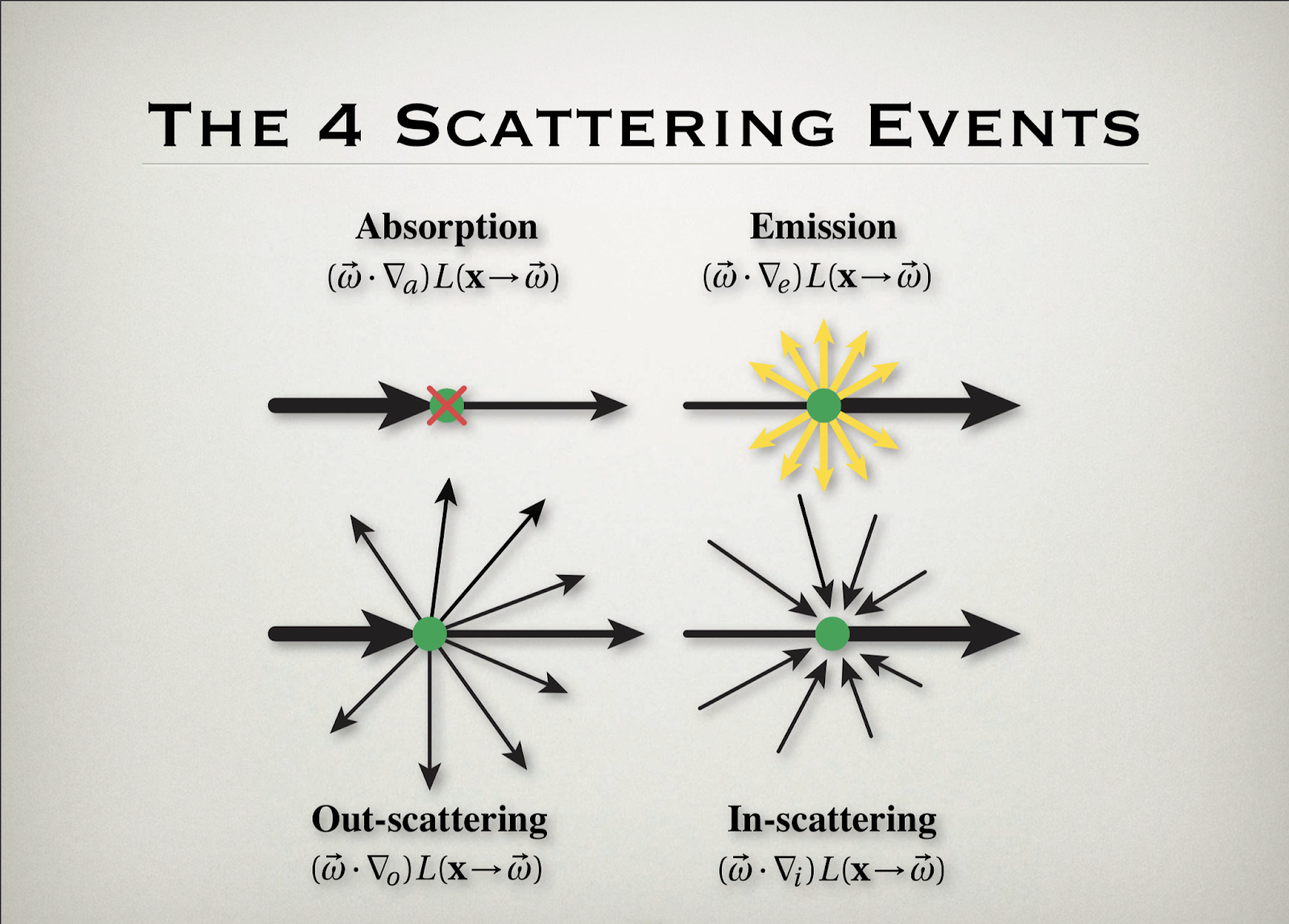
In graphics, we assume that the participating media is a collection of microscopic particles that are randomly positioned, and we do not represent them individually in lighting simulation. Instead, we consider the aggregate probablistic behaviour when light goes through the media. In general, there are four kinds of interaction that can happen during the process: absorption, emission, out-scattering and in-scattering.

When light ray hits particles, some part of the light will be absorbed by the particles, causing the radiance to decrease, and for the same reason of collision, light ray may be out-scattered into various directions. The coefficients of absorption, $\sigma_a$, and scattering, $\sigma_s$, represent the amount of the orginal light that will be absorbed or out-scattered. The two events are also called extinction, and $\sigma_t = \sigma_a + \sigma_s$. $(1 - \sigma_t)$ represents the amount of light that is unaffected and stays on the original path. Radiance can also increase as it travels through the media. Sometimes particles will emit light, such as fire, represented using the coefficient of emission, $\sigma_e$, and lights from other directions may be scattered into the direction that we are currently considering. In this project, we ignore the emission event since the media we are modeling is just air. For the convenience of implementation, we only consider homogeneous media where all the coefficients stay the same throughout the media.

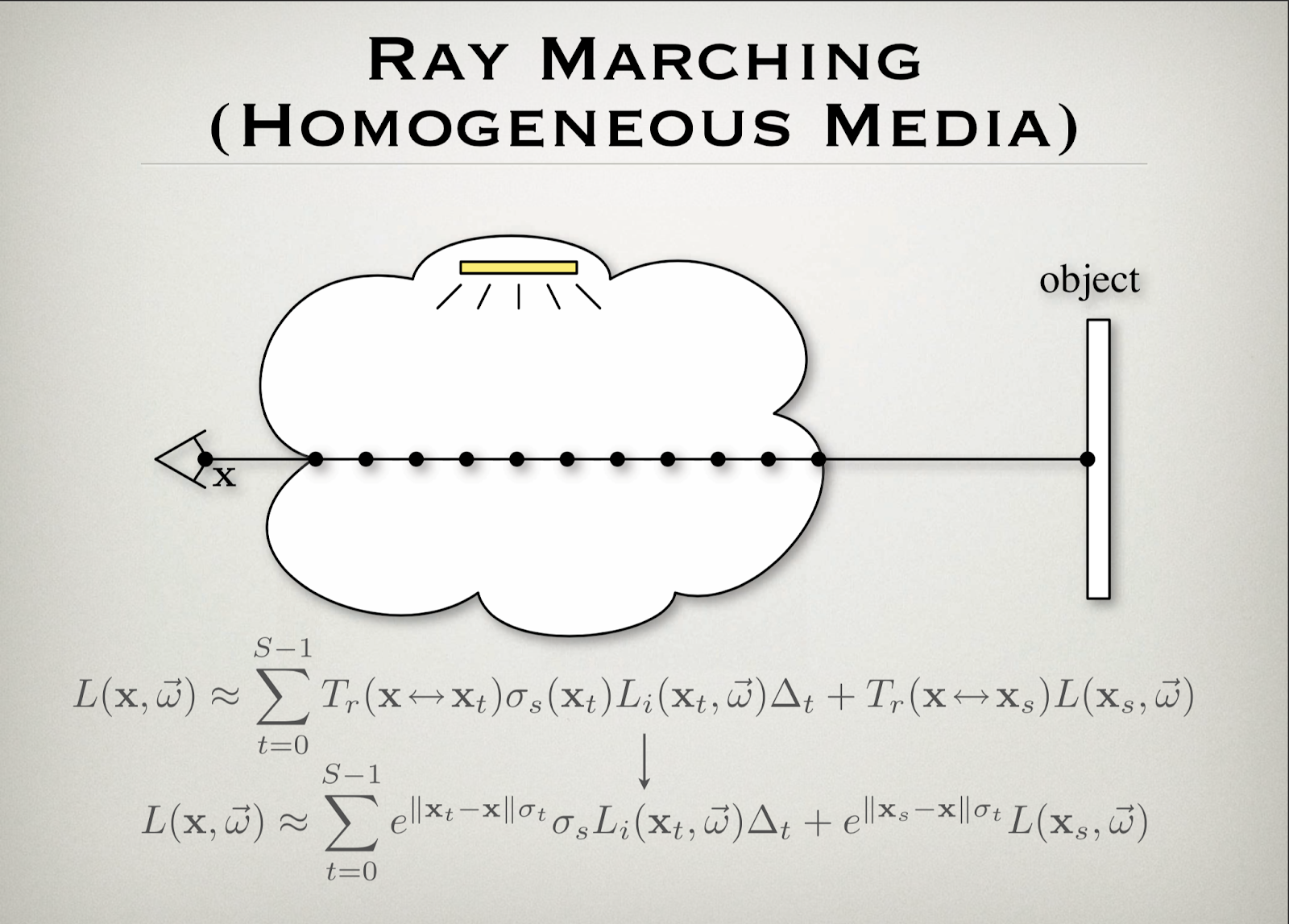
Based on our original path tracer in project3-1, we modified the at_least_one_bounce function by adding scattering term which is the combined radiance of scattering rays whose origins are sampled on the original ray of at_least_one_bounce_radiance function. The scattering term and the original at_least_one_bounce_radiance are summed together with weights equal to the exponential absorbing term to get the final radiance. The basic mathematic formula behind above algorithm is illustrated in image below.

Implementation, problems encountered and solution

• define abs_r as absorption rate, parameter g for Henyey-Greenstein phase function, stride for scattering sampling frequency, fog for reflectance spectrum of fog and ori_sca_ratio for mixing of original radiance and scattering term.

• scattering term:

  • define starting point of the scattering section by randomly initializing a length equal to rand(0, 1) * residual which is the length of the whole original ray % stride.
  • for every stride away from starting point along the direction of original ray, sample a scattering ray whose angle with original ray is decided by Henyey-Greenstein importance sampling with parameter g.
  • for each scattering ray, estimate its radiance and time by exp(-abs_r * distance between origins of scattering ray and original ray)
  • add together all results to get scattering term

• original at_least_one_bounce:

  • for original at_least_one_bounce_radiance, multiply by exp(-abs_r * distance between end and start of original ray) to get original term

At this stage we find out estimating radiance of scattering rays with at_least_one_bounce has little effect, which is the reason why we turn to using est_global_radiance for evaluating scattering terms since this function also contains zero_bounce_radiance. Also we discover that simply adding together original and scattering term is not ideal to generate the effect of gloomy fog, so we create our own parameter ori_sca_ratio which defines the ratio between weight for original term and weight for scattering term. As such, the final result of new at_least_one_bounce is (sca_coef * scatter + ori_coef * ori) * 2. where sca_coef = 1. / (ori_sca_ratio + 1) and ori_coef = 1. - sca_coef.

Interactive Volumetric Path Tracer with OptiX

OptiX

OptiX is a path tracing engine developed by Nvidia. It breaks down path tracing algorithm into a few components. Developers can then customize each component to achieve various effects.

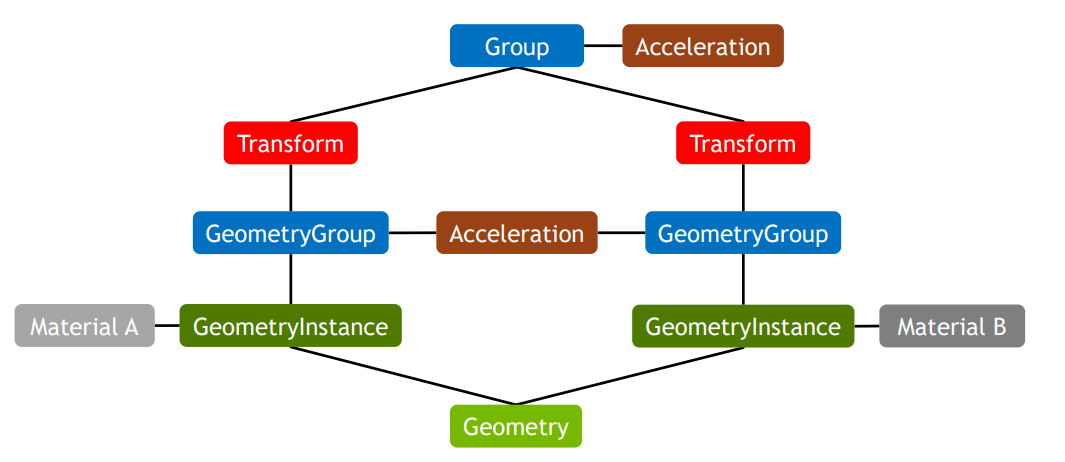
To initialize the engine, we need to create an empty context. We then need to load the scene to the context. As the graph above shows, a scene consists of a number of components. We need to create a few programs to handle each kind of geometry and material. Our goal is to group each primitives correctly so that we can traverse the entire scene from a top node.

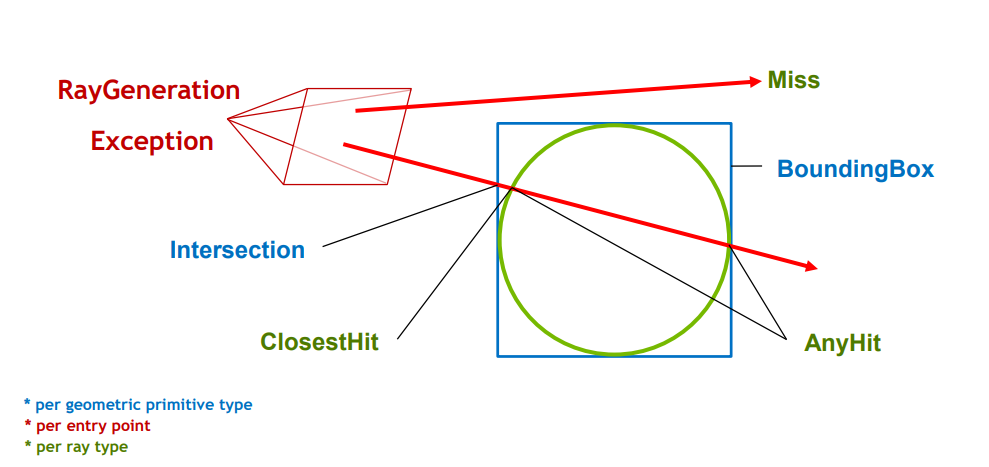
For the scene, BoundingBox and Intersection programs are attached to every instance of a primitive. They are used to tell the engine whether / the time the ray hits an object. When a ray hits an object, ClosestHit program (function as a material) will be called and tell the engine what it should do to the ray, such as changing its radiance or shooting a new ray.

In addition. we need to define some programs for ray. For example, RayGeneration program starts a ray from the camera. Miss program tells the engine what to do when a ray does not hit any objects, such as returning the color of the background.

In our case, we need to implement the Intersection and ClosestHit programs to get volumetric path tracing to work.

Distance Estimate

We use a part of beam radiance estimate algorithm for its simplicity and efficiency.

$t_E$ is the average propagation distance in the medium before getting scattered or absorbed. This simple yet powerful equation can estimate the radiance of a ray in just one single operation so that the costly ray marching is avoided.

Implementation

For Intersection program, we first create a primitive (in our case, a sphere) to define a boundary to contain the medium. When a ray is inside the boundary, for every delta time inside the boundary, we get the position of the hit point and then use the distance estimate to check if the estimated scattering point will be inside the boundary or not. If no, the ray is absorbed. If yes, call ClosestHit program with the estimated scattering point.

The ClosestHit program simply samples each light and shoots a ray in a random direction.

Problems Encountered

• Setting up OptiX was much harder and annoying than we expected. It had to be run in x64 configuration (so incompatible with proj3) but also required specific version of Visual Studio and CUDA. I could not find relevant information online and had to discover these requirements myself. For this project, the setup is OptiX 5.1.1, CUDA 9.0, and VS 2015.
• OptiX is supposed to change the properties of a ray only when it hits an object. This seems automatically makes ray marching algorithm unusable. However, by searching the Internet, we found that we could create a primitive as a boundary and let all the hits happen inside by using the distance estimate.
• There are still some optimizations that can be done to tune the parameters for attenuation when a shadow ray hits the fog.

Results

Raymarching on CPU

Forward scattering

g=0.1	g=0.5

Backward scattering

g=-0.1	g=-0.5

Comparison

g=0.5	g=-0.5

Distance Estimate on GPU

Speed comparison

Video

With / without fog

Without Fog	With Fog

Result

Deliverables

Video

Presentation Slides

Lessons Learned

• The complexity of C++ is depressing. import optix does not exist in C++. Jimmy spent about 50% of his time figuring out how to import OptiX into proj3 (not possible), compile OptiX files, coordinate with GUI, etc.
• Seemingly straightforward mathematical formula and algorithm need to be modified for actual implementation and often times such procedure is full of unexpected obstacles.

References

Volumetric Path Tracing

• Rendering Participating Media
• Tutorial of Ray Casting, Ray Tracing, Path Tracing and Ray Marching
• Volume and Participating Media
• Rendering Participating Media with Bidirectional Path Tracing
• Light Transport in Participating Media
• Monte Carlo Methods for Volumetric Light Transport Simulation
• Volumetric Path Tracing
• The Beam Radiance Estimate for Volumetric Photon Mapping
• Progressive Photon Mapping on GPUs
• Ray Tracing The Next Week

OptiX

• OptiX: A General Purpose Ray Tracing Engine
• OptiX Programming Guide
• OptiX 5.1.1 SDK (available after installing OptiX)
• OptiX Advanced Samples
• Ray Tracing The Next Week in OptiX

Contributions

All

• Project proposal
• Final presentation
• Project report
• Discussed different approaches to implementation

Yin Tang

• Implementing isotropic CPU volumetric path tracing using tracing random walk
• Working with Yi on ray marching

Jimmy Xu

• Set up Nvidia OptiX
• Added modules to a basic OptiX path tracer, such as a sphere primitive
• Implemented volumetric path traicing using distance estimate on OptiX

Yi Zong

• Implementing isotropic CPU volumetric path tracing
• Implementing Henyey-Greenstein CPU volumetric path tracing